This lesson discusses how to calculate the macroscopic dielectric function including excitonic effects within the Bethe-Salpeter (BS) approach. Crystalline silicon is used as test case. A brief description of the formalism can be found in the BS_notes.
The user should be familiarized with the four basic lessons of ABINIT and the first lesson of the GW tutorial, see the tutorial home page.
This lesson should take about one hour to be completed.
Before beginning, you might consider to work in a different subdirectory as for the other lessons. Why not "Work_bs" ?
In the directory ~abinit/tests/tutorial/Input/Work_bs, copy the files file ~abinit/tests/tutorial/Input/tbs_1.files. Now run immediately the calculation with the command:
abinit < tbs_1.files >& tbs_1.log &so that we can analyze the input file while the code is running.
The input file is located in ~abinit/tests/tutorial/Input/tbs_1.in. The header reports a brief description of the calculation so read it carefully. Don't worry if some parts are not clear to you as we are going to discuss the calculation in step by step fashion.
This input file generates the two KSS files and the screening file needed for the subsequent Bethe-Salpeter computations. The first dataset performs a rather standard ground-state calculation on an unshifted 4x4x4 grid (64 k points in the full Brillouin Zone, folding to 8 k points in the irreducible wedge). Then the ground-state density is used in dataset 2 and 3 to generate two KSS files with a standard NSCF cycle, solved with the conjugate-gradient method (kssform=3).
Note that the KSS file computed in dataset 2 contains 100 bands on the 4x4x4 gamma-centered k-mesh whereas the KSS file produced in dataset 3 has only 10 bands on a 4x4x4 k-mesh that has been shifted along the direction
shiftk3 0.11 0.21 0.31 # This shift breaks the symmetry of the k-mesh.The gamma-centered k-mesh contains 8 points in the irreducible zone while the shifted k-mesh breaks the symmetry of the crystal leading to 64 points in the IBZ (actually the IBZ now coincides with the full Brillouin zone). The second mesh is clearly inefficient, so you might wonder why we are using such a bizarre sampling and, besides, why we need to generate two different KSS files!
Indeed this approach strongly differs from the one we followed in the GW tutorials, but there is a good reason for doing so. It is anticipated that optical spectra converge slowly with the Brillouin zone sampling, and that symmetry-breaking k-meshes lead to faster convergence in nkpt than the standard symmetric k-meshes commonly used for ground-state or GW calculations.
This explains the bizarre shift but still why two KSS files? Why don't we simply use the KSS file on the shifted k-mesh to compute the screening?
The reason is that a screening calculation done with many empty bands on the shifted k-mesh would be very memory demanding as the code should allocate a huge portion of memory whose size scales with (nband * nkpt), and no symmetry can be used to reduce the number of k-points.
To summarize: the KSS with the symmetric k-point sampling and 100 bands will be used to compute the screening, while the KSS file with the shifted k-mesh and 10 bands will be used to construct the transition space employed for solving the Bethe-Salpeter equation. The two k-meshes differ just for the shift thus they produce the same set of q-points (the list of q-points in the screening is defined as all the possible differences between the k-points of the KSS file). This means that, in the BS run, we can use the SCR file generated with the symmetric mesh even though the transition space is constructed with the shifted k-mesh.
After this lengthy discussion needed to clarify this rather technical point, we can finally proceed to analyze the screening computation performed in the last dataset of tbs_1.in.
The SCR file is calculated in dataset 4 using nband=100 and ecuteps 6.0 Ha. In the first lesson of the GW tutorial, these values were found to give QP energies converged within 0.01 eV, so we are confident that our SCR file is well converged and it can be safely used for performing convergence tests in the Bethe-Salpeter part.
Note that, for efficiency reasons, only the static limit of W is computed:
nfreqre4 1 # Only the static limit of W is needed for standard BSE calculations. nfreqim4 0Indeed, in the standard formulation of the Bethe-Salpeter equation, only the static limit of the screened interaction is needed to construct the Coulomb term of the BS Hamiltonian. Using a single frequency allows us to save some CPU time in the screening part, but keep in mind that this SCR file can only be used either for Bethe-Salpeter computations or for GW calculations employing the plasmon-pole models corresponding to ppmodel=3,4.
At this point the calculation should have completed, but there's still one thing that we have to do before moving to the next paragraph.
As we said, we will need the KSS file on the shifted k-mesh and the SCR file for our BS calculations so do not delete them! It is also a good idea to rename these precious files using more meaningful names e.g.:
mv tbs_1o_DS2_KSS 444_gamma_KSS mv tbs_1o_DS3_KSS 444_shifted_KSS mv tbs_1o_DS4_SCR 444_SCRKeep in mind that henceforth the k-point sampling cannot be changed anymore: the list of k-points specified in the BS input files MUST equal the one used to generate the KSS file. Two new KSS files and a new SCR file must be generated from scrath if we want to change the k-point sampling used to construct the transition space.
2. Computing the absorption spectrum within the Tamm-Dancoff approximation.
This section is intended to show how to perform a standard excitonic calculation within the Tamm-Dancoff approximation (TDA) using the Haydock iterative technique. The input file is ~abinit/tests/tutorial/Input/tbs_2.in.
Before running the job, we have to connect this calculation with the output results produced in tbs_1.in.
Use the Unix commands:
ln -s 444_shifted_KSS tbs_2i_KSS ln -s 444_SCR tbs_2i_SCRto create two symbolic links for the shifted KSS and the SCR file. The reason for doing so will be clear afterwards once we discuss the input file.
This job lasts 1-2 minutes on a modern machine so it is worth running it before inspecting the input file.
Copy the files file ~abinit/tests/tutorial/Input/tbs_2.files in the working directory and issue
abinit < tbs_2.files >& tbs_2.log &
to put the job in background so that we can examine tbs_2.in.
Now open ~abinit/tests/tutorial/Input/tbs_2.in in your preferred editor and go to the next section where we discuss the most important variables governing a typical BS computation.
First we need to set optdriver=99 to call the BSE routines
optdriver 99 # BS calculationThe variables irdkss and irdscr are similar to other "ird" variables of ABINIT and are used to read the files produced in the previous paragraph
irdkss 1 # Read the KSS file produced in tbs_1 irdscr 1 # Read the SCR file produced in tbs_1The code expects to find an input KSS file and an input SCR file whose name is constructed according to prefix specified in the files file tbs_2.files (see section 1.1 of the abinit_help file). This is the reason why we had to create the two symbolic links before running the code.
Then we have a list of five variables specifying how to construct the excitonic Hamiltonian.
bs_calctype 1 # L0 is constructed with KS orbitals and energies. soenergy 0.8 eV # Scissors operator used to correct the KS band structure. bs_exchange_term 1 # Exchange term included. bs_coulomb_term 11 # Coulomb term included using the full matrix W_GG' bs_coupling 0 # Tamm-Dancoff approximation.The value bs_calctype=1 specifies that the independent-particle polarizability should be costructed with the Kohn-Sham orbitals and energies read from the KSS file. To simulate the self-energy correction, the KS energies are corrected with a scissors operator of energy soenergy= 0.8 eV. This permits us to avoid a cumbersome GW calculation for each state included in our transition space. The use of the scissors operator is a reasonable approximation for silicon but it might fail in more complicated systems in which the GW corrections cannot be simulated in terms of a simple rigid shift of the initial KS bands structure.
The remaining three variables specify how to construct the excitonic Hamiltonian. bs_exchange_term=1 tells the program to calculate the exchage part of the kernel, hence this calculation includes local-field effects. The variable bs_coulomb_term is used to select among different options that are available for the Coulomb term (please take some time to read the description of the variable and the relevant equations in the BS_notes). Finally bs_coupling=0 specifies that the off-diagonal coupling blocks should be neglected (Tamm-Dancoff approximation). This particular combination of parameters thus corresponds to a Bethe-Salpeter calculation within the Tamm-Dancoff approximation with local field effects included.
Then we have the specification of the bands used to construct the transition space:
bs_loband 2 nband 8In this case all the bands around the gap whose index is between 2 and 8 are included in the basis set.
The frequency mesh for the the macroscopic dielectric function is specified through bs_freq_mesh
bs_freq_mesh 0 6 0.02 eV # Frequency mesh.This triplet of real values defines a linear mesh that covers the range [0,6] eV with a step of 0.02 eV. The number of frequency points in the mesh does not have any significant effect on the CPU time, but it is important to stress that the number of bands included in the transition space defines, in conjunction with the number of k-points, the frequency range that can be described. As a consequence bs_loband and nband should be subject to an accurate converge study.
Then we have the parameters that define and control the algorithm employed to calculate the macroscopic dielectric function
bs_algorithm 2 # Haydock method. bs_haydock_niter 100 # Max number of iterations for the Haydock method. bs_haydock_tol 0.05 # Tolerance for the iterative method. zcut 0.15 eV # Complex shift to avoid divergences in the continued fraction.bs_algorithm specifies the algorithm used to calculate the macroscopic dielectric function. In this case we use the iterative Haydock technique whose maximum number of iterations is given by bs_haydock_niter. The iterative algorithm stops when the difference between two consecutive evaluations of the optical spectra is less than bs_haydock_tol. The input variable zcut gives the complex shift to avoid divergences in the continued fraction. From a physical point of view, this parameters mimics the experimental broadening of the absorption peaks. In this test, due to the coarseness of the k-mesh, we have to use a value slightly larger than the default one (0.1 eV) in order to facilitate the convergence of the Haydock algorithm. Ideally, one should make a convergence study decreasing the value of zcut for increasing number of k-points.
The k-point sampling is specified by the set of variables.
# Definition of the k-point grid kptopt 1 # Option for the automatic generation of k points, ngkpt 4 4 4 # This mesh is too coarse for optical properties. nshiftk 1 shiftk 0.11 0.21 0.31 # This shift breaks the symmetry of the k-mesh. chksymbreak 0 # Mandatory for using symmetry-breaking k-meshes in the BS code.The values of kptopt, ngkpt, nshiftk, and shiftk MUST equal the ones used to specify the grid for the KSS file. chksymbreak=0 is used to bypass the check on symmetry breaking that, otherwise, would make the code stop.
The last section of the input file
ecutwfn 8.0 # Cutoff for the wavefunction. ecuteps 2.0 # Cutoff for W and /bare v used to calculate the BS matrix elements. inclvkb 2 # The Commutator for the optical limit is correctly evaluated.specifies the parameters used to calculate the kernel matrix elements and the matrix elements of the dipole operator. We have already encoutered these variables in the first lesson of the GW tutorial so their meaning is (hopefully) familiar to you. A more detailed discussion of the role played by these variables in the BS code can be found in the BS_notes.
The output file, tbs_2.out, reports the basic parameters of the calculation and eventual WARNINGs that are issued if the iterative method does not converge. Please take some time to understand its structure.
Could you answer the the following questions?
After this digression on the main output file, we can finally proceed to analyse the output data of the computation.
The most important results are stored in five different files:
This binary file stores the upper triangle of the resonant block (the matrix is Hermitian hence only the non-redundant part is computed and saved on file). The BSR file can be used to restart the run from a previous computation using the variables getbsreso or irdbsreso. This restart capability is useful for restarting the Haydock method if convergence was not achieved or to execute Haydock computations with different values of zcut. getbsreso and irdbsreso are also handy if one wants to include the coupling on top of a pre-existing TDA calculation since the code uses two different files to store the resonant and the coupling block (BSC is the prefix used for the files storing the coupling term).
It is a binary file containing the results of the Haydock method: the coefficient of the tridiagonal matrix and the three vectors employed in the iterative algorithm. It is usually used to restart the algorithm if convergence has not been achieved (see the related input variables gethaydock and irdhaydock).
The RPA spectrum without local field effects obtained with KS energies and the GW energies, respectively (mnemonics: NLF stands for No Local Field, while MDF stands for Macroscopic Dielectric Function).
Formatted file reporting the macroscopic dielectric function with excitonic effects. Since this file contains the most important results of our calculation it is worth spending some time to discuss its format.
First we have a header reporting the basic parameters of the calculation
# Macroscopic dielectric function obtained with the BS equation. # RPA L0 with KS energies and KS wavefunctions LOCAL FIELD EFFECTS INCLUDED # RESONANT-ONLY calculation # Coulomb term constructed with full W(G1,G2) # Scissor operator energy = 0.8000 [eV] # Tolerance = 0.0500 # npweps = 27 # npwwfn = 283 # nbands = 8 # loband = 2 # nkibz = 64 # nkbz = 64 # Lorentzian broadening = 0.1500 [eV]then the list of q-points giving the direction of the incident photon:
# List of q-points for the optical limit: # q = 0.938821, 0.000000, 0.000000, [Reduced coords] # q = 0.000000, 0.938821, 0.000000, [Reduced coords] # q = 0.000000, 0.000000, 0.938821, [Reduced coords] # q = 0.000000, 0.813043, 0.813043, [Reduced coords] # q = 0.813043, 0.000000, 0.813043, [Reduced coords] # q = 0.813043, 0.813043, 0.000000, [Reduced coords]By default the code calculates the macroscopic dielectric function considering six different directions in q-space (the three basis vectors of the reciprocal lattice and the three Cartesian axis). It is possible to specify custom directions using the input variables gw_nqlwl and gw_qlwl.
Then comes the section with the real and the imaginary part of the macroscopic dielectric as a function of frequency for the different directions:
# omega [eV] RE(eps(q=1)) IM(eps(q=1) RE(eps(q=2) ) ... 0.000 1.8026E+01 0.0000E+00 1.7992E+01 0.0000E+00 1.4292E+01 0.0000E+00 1.3993E+01 0.0000E+00 1.7117E+01 0.0000E+00 1.7080E+01 0.0000E+00 .... .... ...You can visualize the data using your preferred software. For instance,
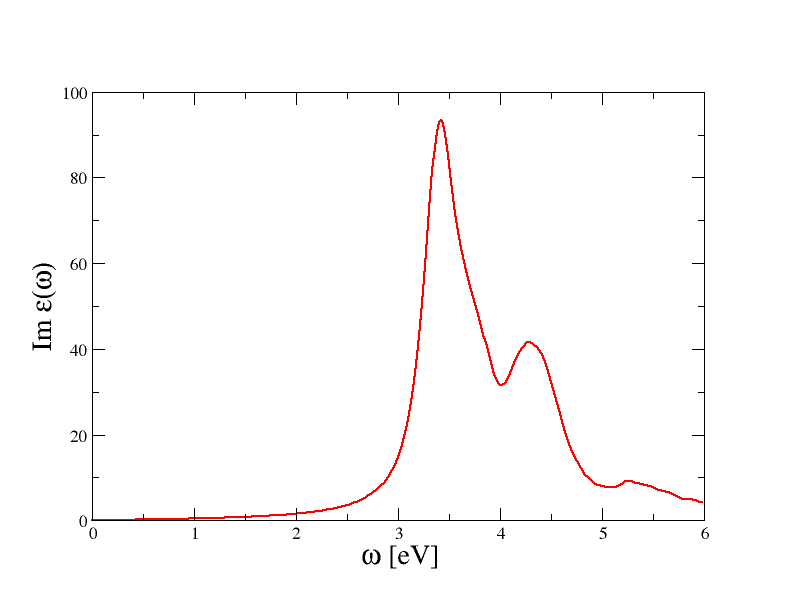
$ gnuplot gnuplot> p "tbs_2o_EXC_MDF" u 1:3 w lwill plot the imaginary part of the macroscopic dielectric function (the absorption spectrum) for the first q-point. You should obtain a graphic similar to the one reported below

Please note that these results are not converged, we postpone the discussion about convergence tests to the next paragraphs of this tutorial.
The most important feature of the spectrum is the presence of two peaks located at around 3.4 and 4.3 eV. To understand the nature of these peaks and the role played by the BS kernel, it is useful to compare the excitonic spectra with the RPA results obtained without local field effects.
Use the sequence of gnuplot command
$ gnuplot gnuplot> p "tbs_2o_EXC_MDF" u 1:3 w l gnuplot> rep "tbs_2o_RPA_NLF_MDF" u 1:3 w l gnuplot> rep "tbs_2o_GW_NLF_MDF" u 1:3 w lto plot the absorption spectrum obtained with the three different approaches. The final result is reported in the figure below.
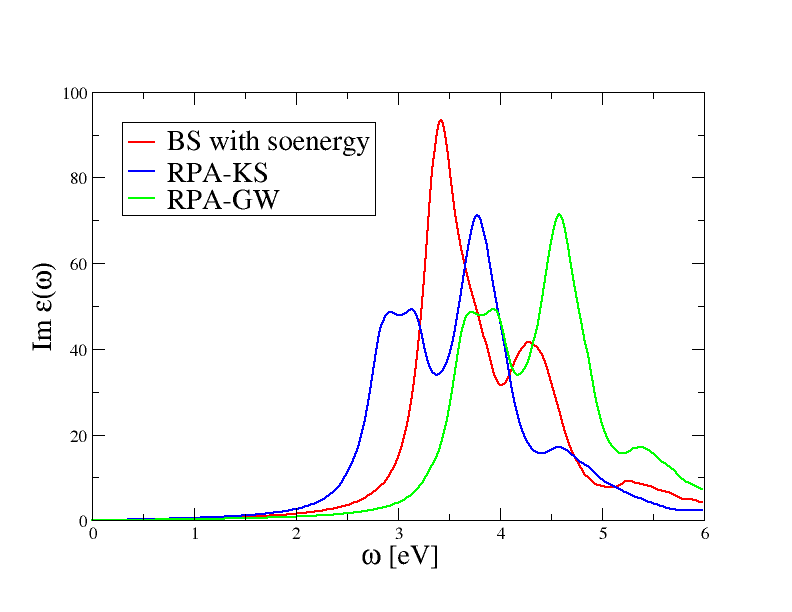
The RPA-KS spectrum underestimates the experimental optical threshold due to the well know band gap problem of DFT. Most importantly, the amplitude of the first peak is underestimated, a problem than is not solved when local-field effects are correctly included in the calculation.
The RPA-GW results with QP corrections simulated with soenergy does not show any significant improvement over RPA-KS: the RPA-GW spectrum is just shifted towards higher frequencies due to opening of the gap, but the shape of the two spectra is very similar, in particular the amplitude of the first peak is still underestimated.
On the contrary, the inclusion of the BS kernel leads to important changes both in the optical threshold as well as in the amplitude of the first peak. This simple analysis tells us that the first peak in the absorption spectrum of silicon has a strong excitonic character that is not correctly described within the RPA. Our first BS spectrum is not converged at all and it barely resembles the experimental result, nevertheless this unconverged calculation is already able to capture the most important physics.
Change the value of the Lorentzian broadening zcut used to avoid divergences in the continued fraction. Then restart the Haydock algorithm from the _BSR and _HAYDR_SAVE files using the appropriate variables. What is the main effect of the broadening on the final spectrum. Does the number of iterations needed to converge depend on the broadening?
Use the appropriate values for bs_exchange_term and bs_coulomb_term to calculate the BS spectrum without local field effects. Compare the results obtained with and without local field effects.
Modify the input file tbs_2.in so that the code reads in the resonant block produced in the previous run and calculates the spectrum employing the method based on the direct diagonalization (use irdbsreso to restart the run but remember to rename the file with the resonant block). Compare the CPU time needed by the two algorithms as a function of the number of transitions in the transition space. Which one has the best scaling?
2.d Preliminary discussion about convergence studies
Converging the excitonic spectrum requires a careful analysis of many different parameters:
Since the memory requirements scale quadratically with the number of k-points in the full Brillouin zone times the number of valence bands times the number of conduction bands included in the transition space, it is very important to find a good compromise between accuracy and computational efficiency.First of all one should select the frequency range of interest since this choice has an important effect on the number of valence and conduction states that have to be included in the transition space. The optical spectrum is expected to converge faster in the number of bands than the GW corrections since only those transitions whose energy is "close" to the frequency range under investigation are expected to contribute.
ecutwfn usually plays a secondary role since it only affects the accuracy of the oscillator matrix elements. We suggest avoiding any truncation of the initial basis set by setting ecutwfn to a value slightly larger than the value of ecut used to generate the KSS file. One should truncate the initial planewave basis set only when experiencing memory problems although this kind of problems can be usually solved by just increasing the number of processors or, alternatively, with an appropriate choice of gwmem.
The value of ecuteps affects the accuracy of the matrix elements of the Coulomb term, the fundamental term that drives the creation of the excitons. As a consequence ecuteps should be subject to an accurate convergence test. As a rule of thumb, ecuteps can be chosen equal or, sometimes, even smaller than the value needed to converge the GW corrections.
As already stated: optical spectra converge slowly with the Brillouin zone sampling. The convergence in the number of k-points thus represents the most important and tedious part of our convergence study. For this reason, this study should be done once converged values for the other parameters have been already found.
3. Convergence with respect to the number of bands in the transition space In this section we take advantage of the multi-dataset capabilities of ABINIT to perform calculations with different values for bs_loband and nband
Before running the test take some time to read the input file ~abinit/tests/tutorial/Input/tbs_3.in.
The convergence in the number of transitions is performed by defining five datasets with different values for nband and bs_loband
ndtset 5 bs_loband1 4 nband1 5 bs_loband2 3 nband2 6 bs_loband3 2 nband3 7 bs_loband4 2 nband4 8 bs_loband5 1 nband5 8
The parameters defining how to build the excitonic Hamiltonian are similar to the ones used in tbs_2.in. The only difference is in the value used for bs_coulomb_term, i.e.
bs_coulomb_term 10 # Coulomb term evaluated within the diagonal approximation.that allows us to save some CPU time during the computation of the Coulomb term.
Also in this case, before running the test, we have to connect tbs_3.in to the KSS and the SCR file produced in the first step. Note that tbs_3.in uses irdkss and irdscr to read the external files, hence we have to create symbolic links for each dataset:
ln -s 444_SCR tbs_3i_DS1_SCR ln -s 444_SCR tbs_3i_DS2_SCR ln -s 444_SCR tbs_3i_DS3_SCR ln -s 444_SCR tbs_3i_DS4_SCR ln -s 444_SCR tbs_3i_DS5_SCR ln -s 444_shifted_KSS tbs_3i_DS1_KSS ln -s 444_shifted_KSS tbs_3i_DS2_KSS ln -s 444_shifted_KSS tbs_3i_DS3_KSS ln -s 444_shifted_KSS tbs_3i_DS4_KSS ln -s 444_shifted_KSS tbs_3i_DS5_KSS
Now we can finally run the the test with
abinit < tbs_3.files >& tbs3.log &This job should last 3-4 minutes so be patient!
Let us hope that your calculation has been completed, and that we can examine the output results.
Use the following sequence of gnuplot commands:
$ gnuplot gnuplot> p "tbs_3o_DS1_EXC_MDF" u 1:3 w l gnuplot> rep "tbs_3o_DS2_EXC_MDF" u 1:3 w l gnuplot> rep "tbs_3o_DS3_EXC_MDF" u 1:3 w l gnuplot> rep "tbs_3o_DS4_EXC_MDF" u 1:3 w l gnuplot> rep "tbs_3o_DS5_EXC_MDF" u 1:3 w lto plot on the same graphic the absorption spectrum obtained with different transition spaces. You should obtain a graphic similar to this one:
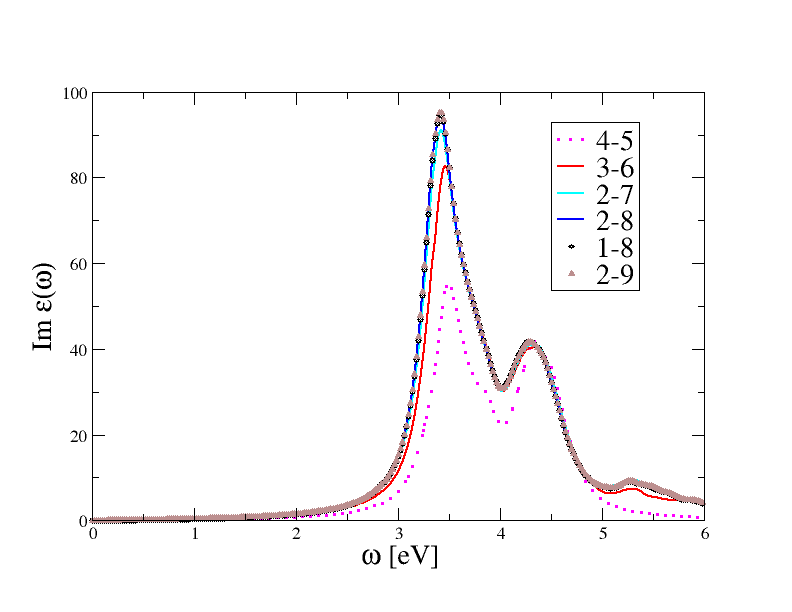
The results obtained with (bs_loband=4, nband=5) are clearly unconverged as the basis set contains too few transitions that are not able to describe the frequency-dependence of the polarizability in the energy range under investigation. For a well converged spectrum, we have to include the three higher occupied states and the first four conduction bands (the blue curve corresponding to bs_loband=2, and nband=8).
Note that adding the first occupied band, curve (1-8), gives results that are almost on top of (2,8). This is due to the fact that, in silicon, the bottom of the first band is located at around 12 eV from the top of the conduction band therefore its inclusion does not lead to any significant improvement of the transition space in the frequency range [0,8] eV. For completeness, we also report the results obtained in a separate calculation done with bs_loband=2 nband=9 to show that four empty states are enough to converge the spectrum.
We therefore fix the number of bands for the transition space using the converged values bs_loband=2, nband=8, and we proceed to analyse the convergence of the spectrum with respect to the number of planewaves in the screening.
The use of irdkss and irdscr is not handy when we have several datasets that are reading the SAME external file as we are forced to use different names for the input of each dataset. To work around this annoyance, one can introduce a fictious dataset (say dataset 99), and let the code use the output of this unexisting dataset as the input of the real datasets. An example will help clarify: Instead of using the lengthy list of links as done before, we might use the much simpler sequence of commands
ln -s 444_shifted_KSS tbs_3o_DS99_KSS ln -s 444_SCR tbs_3o_DS99_SCRprovided that, in the input file, we replace irdkss and irdscr with
getkss 99 # Trick to read the same file tbs_o3_DS99_KSS in each dataset getscr 99 # Same trick for the SCR file
5. Convergence with respect to the number of planewaves in the screening
First of all, before running the calculation, take some time to understand what is done in ~abinit/tests/tutorial/Input/tbs_4.in.
The structure of the input file is very similar to the one of tbs_3.in, the main difference is in the first section:
ndtset 4 ecuteps: 1 ecuteps+ 2 bs_coulomb_term 11that istructs the code to execute four calculations where the direct term is constructed using different value of ecuteps. We also relax the diagonal-only approximation for the screening by setting bs_coulomb_term=11 so that the non-locality of W(r,r') is correctly taken into account.
It is important to stress that it is not necessary to recalculate the SCR file from scratch just to modify the value of ecuteps used in the BS run. The SCR file calculated in the preparatory step contains G-vectors whose energy extends up to ecuteps=6.0 Ha. This is the MAXIMUM cutoff energy that can be used in our convergence tests. If the value of ecuteps specified in the input file is smaller than the one stored on disk, the code will read a sublock of the initial matrix. A WARNING message is issued if the value specified in the input file is larger than the one available in the SCR file.
Now we can finally run the calculation. As usual, we have to copy ~abinit/tests/tutorial/Input/tbs_4.files in the working directory Work_bs, then we have to create a bunch of symbolic links for the input KSS and SCR files:
ln -s 444_SCR tbs_4i_DS1_SCR ln -s 444_SCR tbs_4i_DS2_SCR ln -s 444_SCR tbs_4i_DS3_SCR ln -s 444_SCR tbs_4i_DS4_SCR ln -s 444_shifted_KSS tbs_4i_DS1_KSS ln -s 444_shifted_KSS tbs_4i_DS2_KSS ln -s 444_shifted_KSS tbs_4i_DS3_KSS ln -s 444_shifted_KSS tbs_4i_DS4_KSSNow issue
abinit < tbs_4.files >& tbs4.log &to execute the test (it should take around 2 minutes).
Once the calculation is completed, plot the spectra obtained with different ecuteps using
$ gnuplot gnuplot> p "tbs_4o_DS1_EXC_MDF" u 1:3 w l gnuplot> p "tbs_4o_DS2_EXC_MDF" u 1:3 w l gnuplot> p "tbs_4o_DS3_EXC_MDF" u 1:3 w l gnuplot> p "tbs_4o_DS4_EXC_MDF" u 1:3 w l
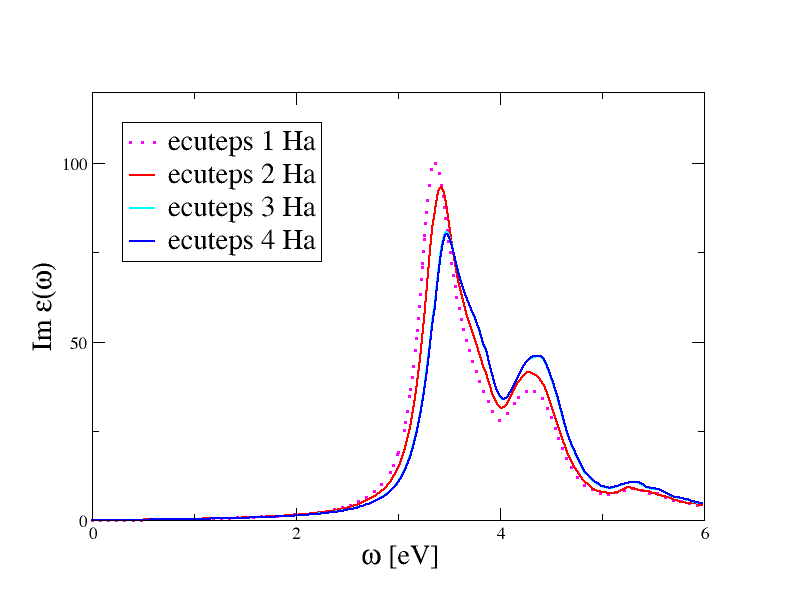
Note that this value is smaller than the one required to converge the QP corrections within 0.01 eV (in the first lesson of the GW tutorial we obtained 6.0 Ha). This is a general behavior, in the sense that Bethe-Salpeter spectra, unlike GW corrections, are not usually very sensitive to truncations in the planewave expansion of W. Reasonable BS spectra are obtained even when W is treated within the diagonal approximation or, alternatively, with model dielectric functions.
Note also how the two peaks are affected in a different way by the change of ecuteps, with the first peak affected the most. This behavior is consistent with our affirmation that the first peak of silicon has a strong excitonic character.
6. Convergence with respect to the number of k-points The last parameter that should be checked for convergence is the number of k-points. This convergence study represents the most tedious and difficult part since it requires the generation of new KSS files and of the new SCR file for each k-mesh (the list of k-points for the wavefunctions and the set of q-points in the screening must be consistent with each other).
The file ~abinit/tests/tutorial/Input/tbs_5.in gathers the different steps of a standard BS calculation (generation of two KSS file, screening calculation, BS run) into a single input. The calculation is done with the converged parameters found in the previous studies, only ngkpt has been intentionally left undefined.
Use tbs_5.in as a template for performing BS calculations with different k-meshes. For example, you might try to compare the three meshes 4x4x4, 5x5x5, and 6x6x6. To facilitate the analysis of the results, we suggest to run the calculations in different directories so that we can keep the output results separated.
Be aware that both the CPU time as well as the memory requirements increase quickly with the number of divisions in the mesh. These are, for example, the CPU times required by different k-meshes on Intel Xeon X5570:
4x4x4: +Overall time at end (sec) : cpu= 112.4 wall= 112.4 5x5x5: +Overall time at end (sec) : cpu= 362.8 wall= 362.8 6x6x6: +Overall time at end (sec) : cpu= 914.8 wall= 914.8 8x8x8: +Overall time at end (sec) : cpu= 5813.3 wall= 5813.3 10x10x10: +Overall time at end (sec) : cpu= 20907.1 wall= 20907.1 12x12x12: +Overall time at end (sec) : cpu= 62738.2 wall= 62738.26x6x6 is likely the most dense sampling you can afford on a single-CPU machine. For you convenience, we have collected the results of the convergence test in the figure below.
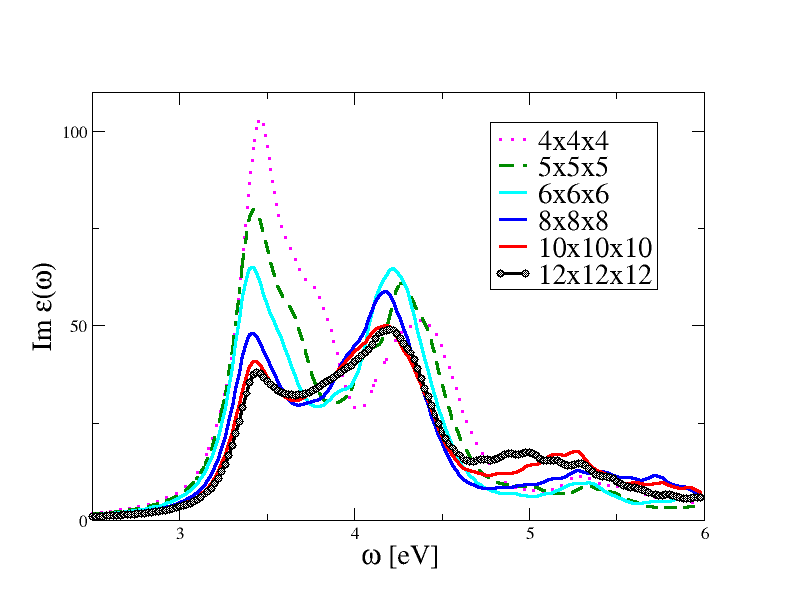
As anticipated, the spectrum converges slowly with the number of k-points and our first calculation done with the 4x4x4 grid is severely unconverged. The most accurate results are obtained with the 12x12x12 k-mesh, but even this sampling leads to converged results only for frequencies below 4.5 eV. This is a problem common to all BS computations, in the sense that it is extremely difficult to achieve global converge in the spectra. This analysis shows that we can trust the 12x12x12 results in the [0:4,5] eV range while the correct description of the spectrum at higher energies would require the inclusion of more k-point and, possibly, more bands so that the band dispersion is correctly taken into account (even the RPA spectrum does not coverge at high frequencies when 12x12x12 is used).
It should be stressed that zcut plays a very important role in these converge tests. For example, the results obtained with the 8x8x8 or the 10x10x10 k-mesh can be brought closer to the 12x12x12 by just increasing the Lorentzian broadening. When comparing theory with experiments, it is common to treat zcut as an a posteriori parameter chosen to produce the best agreement with the experiment.
6. Additional exercises (optional)
Use bs_coupling=1 to perform an excitonic calculation for silicon including the coupling term. Compare the imaginary part of the macroscopic dielectric function obtained with and without coupling. Do you find significant differences? (Caveat: calculations with coupling cannot use the Haydock method and are much more CPU demanding. You might have to decrease some input parameters to have results in reasonable time.)
Calculate the one-shot GW corrections for silicon following the first lesson of the GW tutorial. Then use the _GW file produced by the code to calculate the absorption spectrum.
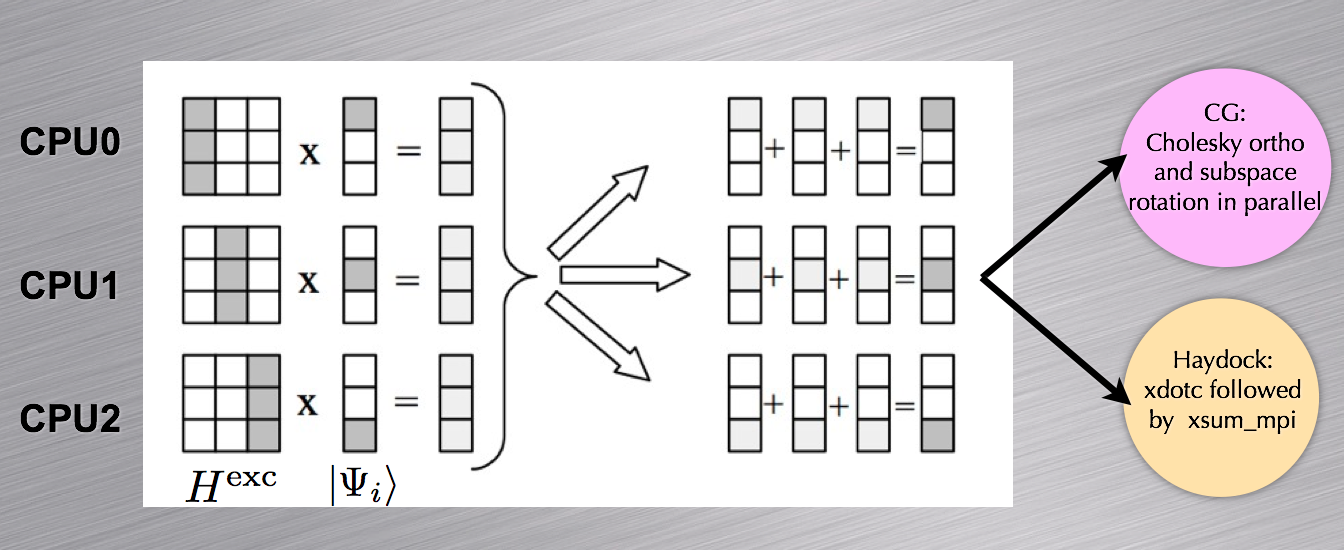
In this section, we discuss the approach used to parallelize the two steps of the BS run, i.e. the construction of the H matrix and the evaluation of the macroscopic dielectric function.
First of all, it is important to stress that, unlike the GW code, the BS routines do not employ any kind of memory distribution for the wavefunctions. The entire set of orbitals used to construct the transition space is stored on each node This choiche has been dictated by the fact that the size of H is usually much larger than the array used to store the wavefunction, hence it is much more important to distribute the matrix than the wavefunctions. Besides, having all the states on each node simplifies the calculation of several intermediate quantities needed at run-time.
The memory allocated for the wavefunctions and the screening thus will not scale with the number of processors. However, for very memory demanding calculations, the real space orbitals can be calculated on the fly with an increase in computational time instead. This option is controlled by the second digit of the input variable gwmem.
When discussing the MPI parallelization of the Bethe-Salpeter routines, we have to consider the two steps separately.
In the first step, the upper triangle of the resonant (coupling) block is distributed among the nodes. Each CPU computes its own portion and stores the results in a temporary array. At the end of the computation, the portions of the upper triangle are communicated to the master node which writes the binary file BSR (BSC).
In the second step, each node reads the data stored in the external files in order to build the excitonic Hamiltonian. The matrix is distributed using a column-block partitioning, so that the matrix-vector multiplications required in the Haydock iterative scheme can be easily performed in parallel (see the schematic representation reported below). A similar distribution scheme is also employed for the conjugate-gradient minimization. For a balanced distribution of computational work, the number of processors should divide the total number of resonant transitions.