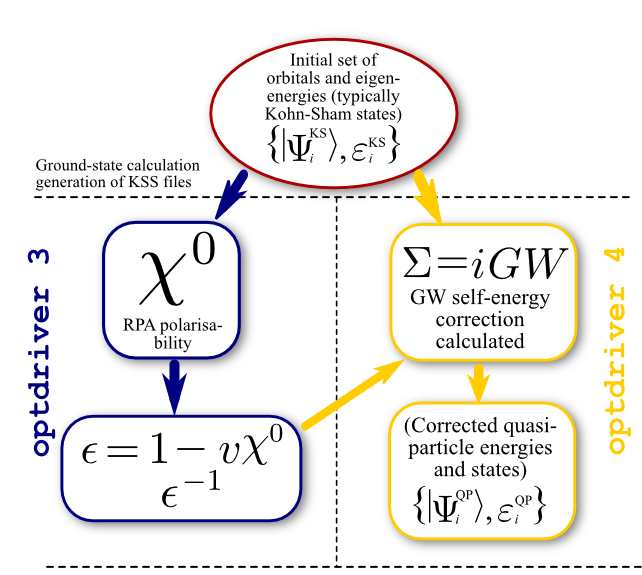
This lesson aims at showing how to calculate self-energy corrections to the DFT Kohn-Sham eigenvalues in the GW approximation.
A brief description of the formalism and of the equations implemented in the code can be found in the GW_notes.
The different formulas of the GW formalism have been written in a pdf document by Valerio Olevano (who also wrote the first version of this tutorial), see ~abinit/doc/theory/gwa.pdf .
For a much more consistent discussion of the theoretical aspects of the GW method we refer the reader to the review
It is suggested to
acknowledge the efforts of developers of the GW part of ABINIT, by citing
X. Gonze, G.-M. Rignanese, M. Verstraete, J.-M. Beuken, Y. Pouillon,
R. Caracas, F. Jollet, M. Torrent, G. Zerah, M. Mikami, Ph. Ghosez,
M. Veithen, J.-Y. Raty, V. Olevano, F. Bruneval, L. Reining,
R. Godby, G. Onida, D.R. Hamann, and D.C. Allan.
Zeit. Kristallogr. 220, 558-562 (2005).
The user should be familiarized with the four basic lessons of ABINIT, see the tutorial home page.
After this first tutorial on GW, you should read the second tutorial on GW.
This lesson should take about 2 hours.
Before beginning, you might consider to work in a different subdirectory as for the other lessons. Why not "Work_gw1" ?
At the end of lesson 3, we computed the Kohn-Sham band structure of silicon. In this approximation, the band dispersion as well as the band widths are reasonable, but the band gaps are qualitatively wrong. Now, we will compute the band gaps much more accurately, using the so-called GW approximation.
We start by an example, in which we show how to perform in a single input file the calculation of the ground state density, the Kohn Sham band structure, the screening, and the the GW corrections. We use reasonable values for the parameters of the calculation. The discussion on the convergence tests is postponed to the next paragraphs. We will see that GW calculations are MUCH MORE time-consuming than the computation of the Kohn-Sham eigenvalues.
So, let us run immediately this calculation, and while it is running, we will explain what has been done.
In the directory ~abinit/tests/tutorial/Input/Work_gw1, copy the files ~abinit/tests/tutorial/Input/tgw1_x.files and tgw1_1.in, and modify the tgw1_x.files file as usual (see lesson 1).
Then, issue:
abinit < tgw1_x.files >& tgw1_1.log &
It is very important to run this job in background. Indeed, a PC Intel PIV/2.2 GHz will take about 6 minutes to complete it. In the meantime, you should read the following.
In order to perform a standard one-shot GW calculation one has to:

The first dataset performs a rather usual SCF calculation and produces a specialized file, tgw1_xo_DS1_KSS (_KSS stands for Kohn-Sham Structure), that contains the information needed to start step 2. The second dataset drives the computation of susceptibility and dielectric matrices, producing another specialized file, tgw1_xo_DS2_SCR (_SCR for "Screening", actually the inverse dielectric matrix ε-1). Then, in the third dataset, the code calculates the quasiparticle energies for the 4th and 5th bands at the Γ point.
So, you can edit this tgw1_1.in file.
The dataset-independent part of this file (the last half of the file), contains the usual set of input variables describing the cell, atom types, number, position, planewave cut-off energy, SCF convergence parameters driving the Kohn-Sham band structure calculation. Then, for the three datasets, you will find specialized additional input variables.
In dataset 1, apart from the usual input variables we are acquainted to through the previous tutorials, there is a new input variable:
nbandkss -1 # Number of bands in KSS file (-1 means the maximum possible)
This input variable tells the program to calculate the Kohn-Sham electronic structure by perforing the full diagonalization of the Kohn-Sham Hamiltonian evaluated at the converged density and calculated in each one of the k-points of the grid. Note that this diagonalization is performed in a routine (outkss.F90) separated from the usual SCF cycle, so that there is additional control of the wavefunction actually stored, if needed. In particular, the number of bands to be computed in this routine is NOT determined by the usual input variable nband.
nbandkss is the key variable to create a _KSS file. If it is zero, no _KSS file will be created. -1 lead to the generation (full diagonalization of the Kohn-Sham hamiltonian) and storage of the maximum possible number of states (or bands) common to all points. This depends on the energy cutoff ecut which also determines the dimension of the Kohn-Sham hamiltonian, and might lead to quite time-consuming calculations. One can reduce the load in the diagonalization by requiring less states by carring out partial diagonalizations of the Kohn-Sham hamiltonian. This can be done by the use of kssform=3, and is to be preferred when the number of planewaves is getting large, see later (try both kssform=1 and kssform=3 when you start calculations beyond the tutorial).
The variable npwkss governs the size of the plane wave basis used to store the wavefunctions in the KSS file. The default value leaves the number of plane waves equal to the one of the SCF ground state calculation determined by the ecut variable. The variable npwkss reduces the size of the KSS file but it does NOT reduce the load of the diagonalization since the dimension of the Kohn-Sham hamiltonian is always controlled by ecut and npwkss acts only as a post-diagonalization cutoff. Please also notice that in the GW calculation the plane waves basis is always Γ centered and it is the same for all the considered k-points, while in the Ground State calculation the plane waves basis changes for each k-point, each time being centered on the given k-point.
Another relevant input variable, related also to the specific set up of the _KSS file is kssform. In this case we are using the value 1, which corresponds to ask a KSS (Kohn-Sham electronic Structure file) through a diagonalization of the Kohn-Sham hamiltonian. The value 3 corresponds to ask a KSS through the normal Conjugate Gradient algorithm to be carried out also for all the empty states we need in the GW calculation (in much the same way of what is done when calculating a band plot, paying attention at the value used for the tolerance on the residual on the wavefunctions). This could be interesting for systems having very large Kohn-Sham Hamiltonians, that is very large cutoff energies. However, if the number of states needed in the GW calculation is large, it might be more convenient to carry out the diagonalization even in this case.
In this first dataset, we asked also the self-consistent cycle to be done for nine bands.
nband1 9 # Number of (occ and empty) bands to be computedOnly four bands would be needed for Si. The purpose of defining more bands in the ground-state run is to verify that at least the first Kohn-Sham eigenvalues obtained through the diagonalization are sufficiently close to those determined (with a residual) in the self-consistent procedure. The comparison is done automatically, and one should check if there is something wrong when a warning message appears.
Finally, the input variable symmorphi is also used in this datafile, where it is set to 0. Please, read the corresponding section of the help file. This restriction of symmetry operations to symmorphic ones for the GW part has been waived since the tutorial was originally written. For your production runs, please use (symmorphi=1) whenever you generate the KSS file, or perform the calculation of the screening or the self-energy.
In dataset 2, the calculation of the screening (susceptibility, dielectric matrix) is performed. We need to set optdriver=3 to do that:
optdriver2 3 # Screening calculation
The getkss input variable is similar to other "get" input variables of ABINIT :
getkss2 -1 # Obtain KSS file from previous datasetIn this case, it tells the code to use the KSS file calculated in the previous dataset.
Then, three input variables describe the computation :
nband2 25 # Bands used in the screening calculation ecutwfn2 2.1 # Cut-off energy of the planewave set to represent the wavefunctions ecuteps2 3.6 # Cut-off energy of the planewave set to represent the dielectric matrixIn this case, we use 25 bands to calculate the Kohn-Sham response function $\chi^{(0)}_{KS}$. We use a cut-off ecutwfn=2.1 Hartree, giving 89 planewaves to represent the wavefunctions in the calculation of $\chi^{(0)}_{KS}$. The dimension of $\chi^{(0)}_{KS}$, as well as all the other matrices ($\chi$, $\epsilon$) is determined by ecuteps=3.6 Hartree, giving 169 planewaves.
Finally, we define the frequencies at which the screening must be evaluated: ω=0.0 eV and the imaginary frequency ω= i 16.7 eV. The latter is determined by the input variable ppmfrq
ppmfrq2 16.7 eV # Imaginary frequency where to calculate the screeningThe two frequencies are used to calculate the plasmon-pole model parameters. For the non-zero frequency it is recommended to use a value close to the plasmon frequency for the plasmon-pole model to work well. Plasmons frequencies are usually close to 0.5 Hartree. The parameters for the screening calculation are not far from the ones that give converged Energy Loss Function (-Im \epsilon^-1_00) spectra, So that one can start up by using indications from EELS calculations existing in literature.
In dataset 3 the calculation of the Self-Energy matrix elements is performed. One needs to define the driver option, as well as the _KSS and _SCR files.
optdriver3 4 # Self-Energy calculation getkss3 -2 # Obtain KSS file from dataset 1 getscr3 -1 # Obtain SCR file from previous datasetThe getscr input variable is similar to other "get" input variables of ABINIT.
Then, comes the definition of parameters needed to compute the self-energy. As for the computation of the susceptibility and dielectric matrices, one must define the set of bands, and two sets of planewaves:
nband3 100 # Bands to be used in the Self-Energy calculation
ecutwfn3 5.0 # Planewaves to be used to represent the wavefunctions
ecutsigx3 6.0 # Dimension of the G sum in Sigma_x
# (the dimension in Sigma_c is controlled by npweps)
In this case,
nband
controls the number of bands used to calculate the correlation part of the Self-Energy.
ecutwfn
defines (as for
optdriver=3)
the number of planewaves used to represent the wavefunctions.
ecutsigx
gives the number of planewaves used to calculate σx (the exchange part of the self-energy).
The size of the planewave set used to compute Σc (the correlation part of the self-energy) is controlled by
ecuteps
(cannot be larger than the value used to generate the SCR file).
However, it is taken equal to the number of planewave of Σx if the latter is smaller than the one for Σc.
Then, come the parameters defining the k-points and the band indices for which the quasiparticle energies will be computed:
nkptgw3 1 # number of k-point where to calculate the GW correction kptgw3 # k-points -0.125 0.000 0.000 bdgw3 4 5 # calculate GW corrections for bands from 4 to 5
There is an additional parameter, called zcut, related to the self-energy computation. It is meant to avoid some divergencies that might occur in the calculation due to integrable poles along the integration path.
Let us hope that your calculation has been completed, and that we can examine the output file. Open tgw1_1.out in your preferred editor.
The first departure from the usual information present in the output file for usual GS calculations appears after the SCF cycles of DATASET 1 :
====================================================================== Calculating and writing out Kohn-Sham electronic Structure file Using diagonalized wavefunctions and energies (kssform=1) number of Gamma centered plane waves 471 number of Gamma centered shells 40 number of bands 283 maximum angular momentum components 3This section was issued when the Hamiltonian at the different k points was diagonalized, after the SCF cycles, in order to generate the KSS file. Then, comes the output of the numerous eigenvalues at the different k-points. Finally, the normalisation and orthogonalisation of the eigenvectors is tested. One should obtain close to perfect normalisation and orthogonalisation at that stage :
Test on the normalization of the wavefunctions min sum_G |a(n,k,G)| = 1.000000 max sum_G |a(n,k,G)| = 1.000000 Test on the orthogonalization of the wavefunctions min sum_G a(n,k,G)* a(n',k,G) = 0.000000 max sum_G a(n,k,G)* a(n',k,G) = 0.000000Of course, if we post-cutoff the wavefunctions by using a reduced value for npwkss this results in a reduction in the orthonormalization of the wavefunctions.
Then, follows the usual information for the dataset 1. The second dataset drives the computation of the susceptibility and dielectric matrices, in preparation of the GW energy calculation done in dataset 3. After some general information (origin of KSS file, header, description of unit cell), comes the echo of Kohn-Sham eigenenergies (in eV), and then the evaluation of the wavefunction normalisation and orthogonalisation USING ONLY THE PLANEWAVE SET DEFINED BY ecutwfn, npwwfn, or nshwfn. Thus, there is no surprise that these relations are not fulfilled:
test on the normalization of the wavefunctions min sum_G |a(n,k,G)| = 0.497560 max sum_G |a(n,k,G)| = 0.995840 test on the orthogonalization of the wavefunctions min sum_G a(n,k,G)* a(n",k,G) = 0.000000 max sum_G a(n,k,G)* a(n",k,G) = 0.179458The squared norm of one of the wavefunctions is even as low as one half! This should lead us to question the choice of ecutwfn that we have made. One should do a convergence study, see later. With the increase of memory/disk space, in the last years, it appears that in most of the cases, it is fine to set ecutwfn to the maximal value, that is ecut, which has become the default value.
The parameters of the FFT grid needed to represent the wavefunctions and to compute their convolution (so as to get the screening matrices) are then given.
Then, the grid of q-point (in the Irreducible part of the Brillouin Zone) on which the susceptibility and dielectric matrices will be computed is given. It is a set of BZ points defined as all the possible differences among the k-points (q=k-k') of the grid chosen to generate the KSS file. From the last statement it is clear the interest to choose homogenous k-point grids, in order not to explose the number of q-points.
On the basis of only the average density, one can obtain the classical Drude plasmon frequency. The next lines calculate the average density of the system, and evaluate the r_s parameter, then compute the Drude plasmon frequency. This is the value used by default for the parameter ppmfrq. It is in fact the second frequency where the code calculates the dielectric matrix to adjust the plasmon-pole model parameters. It has been found that Drude plasma frequency is a reasonable value where to adjust the model. The control over this parameter is however left to the user in order to check that the result does not change when changing ppmfrq. If it is the case, then the plasmon-pole model is not appropriated and one should go beyond by taking into account a full dynamical dependence in the screening (see later, the contour-deformation method). However, the plasmon-pole model has been found to work well for a very large range of systems when focusing only on the real part of the GW corrections.
At the end of the screening calculation, the macroscopic dielectric constant is printed:
dielectric constant = 13.8483 dielectric constant without local fields = 15.5527Note that the convergence in the dielectric constant DOES NOT guarantee the convergence in the GW corrections. In fact, the dielectric constant is representative of only one element i.e. the head of the full dielectric matrix. Even if the convergence on the dielectric constant with local fields takes somehow into account also other non-diagonal elements. In a GW calculation all the ε-1 matrix is used to build the Self-Energy operator.
We enter now the third dataset. As for dataset 2, after some general information (origin of KSS file, header, description of unit cell), the echo of Kohn-Sham eigenenergies (in eV), the evaluation of the wavefunction normalisation, the description of the FFT grid and jellium parameters, there is the echo of parameters for the plasmon-pole model, and the inverse dielectric function (the screening). The self-energy operator has been constructed, and one can evaluate the GW energies, for each of the states.
The results follows :
k = -0.125 0.000 0.000
Band E0 <VxcLDA> SigX SigC(E0) Z dSigC/dE Sig(E) E-E0 E
4 5.616 -11.115 -12.334 1.257 0.775 -0.290 -11.085 0.030 5.646
5 8.357 -10.140 -5.951 -3.336 0.779 -0.284 -9.476 0.664 9.021
E^0_gap 2.741
E^GW_gap 3.375
DeltaE^GW_gap 0.634
For the desired k-point, state 4, then state 5, one finds different information:
It is seen that the average Kohn-Sham exchange-correlation potential for the state 4 (a valence state) is very close to the exchange self-energy correction. For that state, the correlation correction is small, and the difference between Kohn-Sham and GW energies is also small (43 meV). By contrast, the exchange self-energy is much smaller than the average Kohn-Sham potential for the state 5 (a conduction state), but the correlation correction is much larger than for state 4. On the whole, the difference between Kohn-Sham and GW energies is not very large, but nevertheless, it is quite important when compared with the size of the gap.
2 Preparing convergence studies : Kohn-Sham structure (KSS file) and screening (SCR file). In the following sections, we will perform different convergence studies. In order to keep the CPU time at a reasonable level, we will use fake KSS and screening data. Moreover we will only consider the correction at the Γ point only. In this way, we will be able to verify convergence aspects that could be very cumbersome (at least in the framework of a tutorial) if more k-points were used. Testing the convergence with a Γ point only grid of k point represents a convenient approach although some caution should always be used.
In directory ~abinit/tests/tutorial/Input/Work_gw1, copy the file ../tgw1_2.in, and modify the tgw1_x.files file as usual. Edit the tgw1_2.in file, and take the time to examine it. Note that the SCF cycles have been disconnected from the generation of the KSS file.
Then, issue:
abinit < tgw1_x.files >& tgw1_2.log &This small job lasts about 10 secs on a PC PIV Intel 2.2 GHz.
After this step you will need the KSS and SCR files produced in this run for the next runs (up to 6.8). Move tgw1o_DS2_KSS to tgw1o_DS1_KSS and tgw1o_DS3_SCR to tgw1o_DS1_SCR.
The next sections are intended to show you how to find the converged parameters for a GW calculation. In principle, the following parameters might be used to decrease the CPU time or memory demand: optdriver=3 ecutwfn, ecuteps, nband. and for optdriver=4, ecutwfn, ecutsigx, nband.
Before 2008, the advice was indeed to check independently what was the best value for each of these. However, with the evolution of memory/disk space, as well as the advent of new techniques to diminish the number of bands that is needed (see e.g. F. Bruneval, X. Gonze, Phys. Rev. B 78, 085125 (2008), and the input variable gwcomp), standard calculations nowadays only need the tuning of nband ecuteps, simultaneously for optdriver=3 and =4. Indeed, ecutwfn and can have the default value of ecut, while ecutsigx can have the default value of 4*ecut for norm-conserving pseudopotentials, or pawecutdg for PAW calculations. Actually, the present tutorial needs to be updated to account for the current practice.
We begin by the convergence study on the three parameters needed in the self-energy calculation (optdriver=4): ecutwfn, ecutsigx, nband. This is because for these, we will not need a double dataset loop to check this convergence, and we will rely on the previously determined SCR file.
3 Convergence on the number of planewaves in the wavefunctions to calculate the Self-Energy (optional). First, we check the convergence on the number of planewaves used to describe the wavefunctions, in the calculation of the Self-Energy. This will be done by defining five datasets, with increasing ecutwfn:
ndtset 5 ecutwfn: 3.0 ecutwfn+ 1.0
In directory ~abinit/tests/tutorial/Input/Work_gw1, copy the file ../tgw1_3.in, and modify the tgw1_x.files file as usual. Edit the tgw1_3.in file, and take the time to examine it.
Then, issue:
abinit < tgw1_x.files >& tgw1_3.log &This small job lasts about 10 secs on a PC PIV Intel 2.2 GHz.
Edit the output file. The number of plane waves used for the wavefunctions in the computation of the self-energy is mentioned in the fragments of output :
SIGMA fundamental parameters: PLASMON POLE MODEL number of plane-waves for SigmaX 169 number of plane-waves for SigmaC and W 169 number of plane-waves for wavefunctions 59
Gathering the GW energies for each planewave set, one gets :
number of plane-waves for wavefunctions 59
Band E0 VxcLDA SigX SigC(E0) Z dSigC/dE Sig(E) E-E0 E
4 5.915 -11.637 -15.237 3.897 0.806 -0.240 -11.398 0.239 6.154
5 8.445 -9.653 -3.222 -5.460 0.819 -0.222 -8.858 0.795 9.240
number of plane-waves for wavefunctions 113
Band E0 VxcLDA SigX SigC(E0) Z dSigC/dE Sig(E) E-E0 E
4 5.915 -11.639 -15.244 3.789 0.804 -0.244 -11.492 0.148 6.063
5 8.445 -9.675 -3.213 -5.564 0.817 -0.224 -8.941 0.734 9.179
number of plane-waves for wavefunctions 137
Band E0 VxcLDA SigX SigC(E0) Z dSigC/dE Sig(E) E-E0 E
4 5.915 -11.639 -15.244 3.779 0.804 -0.244 -11.499 0.139 6.055
5 8.445 -9.686 -3.216 -5.577 0.817 -0.225 -8.957 0.730 9.175
number of plane-waves for wavefunctions 169
Band E0 VxcLDA SigX SigC(E0) Z dSigC/dE Sig(E) E-E0 E
4 5.915 -11.636 -15.242 3.770 0.804 -0.245 -11.505 0.132 6.047
5 8.445 -9.701 -3.221 -5.584 0.817 -0.225 -8.970 0.732 9.177
number of plane-waves for wavefunctions 259
Band E0 VxcLDA SigX SigC(E0) Z dSigC/dE Sig(E) E-E0 E
4 5.915 -11.652 -15.253 3.766 0.803 -0.245 -11.519 0.133 6.048
5 8.445 -9.700 -3.219 -5.591 0.816 -0.225 -8.974 0.726 9.172
So that ecutwfn=5.0 (npwwfn=137) can be considered converged within 0.01eV.
4 Convergence on the number of planewaves to calculate Σx (optional).
Second, we check the convergence on the number of planewaves in the calculation of Σx. As mentioned in the documentation ecutsigx, safe values exist for ecutsigx, so that if you do not want to squeeze the CPU time for your calculation (you might gain only a few percent in some cases ...), you can impose these values, and skip the corresponding convergence study.
In this lesson, this convergenc study will be done by defining five datasets, with increasing ecutsigx:
ndtset 7 ecutsigx: 3.0 ecutsigx+ 1.0
In directory ~abinit/tests/tutorial/Input/Work_gw1, copy the file ../tgw1_4.in, and modify the tgw1_x.files file as usual. Edit the tgw1_4.in file, and take the time to examine it.
Then, issue :
abinit < tgw1_x.files >& tgw1_4.log &This small job lasts about 12 secs on a PC PIV Intel 2.2 GHz.
Edit the output file. The number of plane waves used for Σx is mentioned in the fragments of output:
SIGMA fundamental parameters: PLASMON POLE MODEL number of plane-waves for SigmaX 59 number of plane-waves for SigmaC and W 59
Gathering the GW energies for each planewave set, one gets :
number of plane-waves for SigmaX 59
number of plane-waves for SigmaC and W 59
Band E0 VxcLDA SigX SigC(E0) Z dSigC/dE Sig(E) E-E0 E
4 5.915 -11.639 -15.195 3.862 0.806 -0.241 -11.392 0.247 6.162
5 8.445 -9.686 -3.177 -5.595 0.818 -0.223 -8.938 0.748 9.193
number of plane-waves for SigmaX 113
number of plane-waves for SigmaC and W 113
Band E0 VxcLDA SigX SigC(E0) Z dSigC/dE Sig(E) E-E0 E
4 5.915 -11.639 -15.235 3.795 0.804 -0.244 -11.479 0.160 6.075
5 8.445 -9.686 -3.210 -5.581 0.817 -0.224 -8.955 0.731 9.176
number of plane-waves for SigmaX 137
number of plane-waves for SigmaC and W 137
Band E0 VxcLDA SigX SigC(E0) Z dSigC/dE Sig(E) E-E0 E
4 5.915 -11.639 -15.241 3.785 0.804 -0.244 -11.492 0.147 6.062
5 8.445 -9.686 -3.213 -5.577 0.817 -0.224 -8.955 0.732 9.177
number of plane-waves for SigmaX 169
number of plane-waves for SigmaC and W 169
Band E0 VxcLDA SigX SigC(E0) Z dSigC/dE Sig(E) E-E0 E
4 5.915 -11.639 -15.244 3.779 0.804 -0.244 -11.499 0.139 6.055
5 8.445 -9.686 -3.216 -5.577 0.817 -0.225 -8.957 0.730 9.175
number of plane-waves for SigmaX 259
number of plane-waves for SigmaC and W 169
Band E0 VxcLDA SigX SigC(E0) Z dSigC/dE Sig(E) E-E0 E
4 5.915 -11.639 -15.247 3.779 0.804 -0.244 -11.501 0.138 6.053
5 8.445 -9.686 -3.218 -5.577 0.817 -0.225 -8.958 0.728 9.173
number of plane-waves for SigmaX 283
number of plane-waves for SigmaC and W 169
Band E0 VxcLDA SigX SigC(E0) Z dSigC/dE Sig(E) E-E0 E
4 5.915 -11.639 -15.247 3.779 0.804 -0.244 -11.501 0.138 6.053
5 8.445 -9.686 -3.218 -5.577 0.817 -0.225 -8.958 0.728 9.173
number of plane-waves for SigmaX 283
number of plane-waves for SigmaC and W 169
Band E0 VxcLDA SigX SigC(E0) Z dSigC/dE Sig(E) E-E0 E
4 5.915 -11.639 -15.247 3.779 0.804 -0.244 -11.501 0.138 6.053
5 8.445 -9.686 -3.218 -5.577 0.817 -0.225 -8.958 0.728 9.173
So that ecutsigx=6.0 (npwsigx=169) can be considered converged within 0.01eV.
5 Convergence on the number of bands to calculate Σc (important).
At last, as concerns the computation of the self-energy, we check the convergence on the number of bands in the calculation of Σc. This convergence study is rather important, usually, BUT it can be done at the same time as the convergence study for the number of bands for the dielectric matrix.
The convergence on the number of bands to calculate the Self-Energy will be done by defining five datasets, with increasing nband:
ndtset 5 nband: 50 nband+ 50
In directory ~abinit/tests/tutorial/Input/Work_gw1, copy the file
../tgw1_5.in, and modify the tgw1_x.files file as usual.
Edit the tgw1_5.in file, and take the time to examine it.
Then, issue :
abinit < tgw1_x.files >& tgw1_5.log &This small job lasts about 12 secs on a PC PIV Intel 2.2 GHz.
Edit the output file. The number of bands used for the self-energy is mentioned in the fragments of output:
SIGMA fundamental parameters: PLASMON POLE MODEL number of plane-waves for SigmaX 169 number of plane-waves for SigmaC and W 169 number of plane-waves for wavefunctions 137 number of bands 50
Gathering the GW energies for each number of bands, one gets :
number of bands 50
4 5.915 -11.639 -15.244 3.853 0.804 -0.243 -11.440 0.199 6.114
5 8.445 -9.686 -3.216 -5.507 0.817 -0.224 -8.899 0.787 9.232
number of bands 100
4 5.915 -11.639 -15.244 3.779 0.804 -0.244 -11.499 0.139 6.055
5 8.445 -9.686 -3.216 -5.577 0.817 -0.225 -8.957 0.730 9.175
number of bands 150
4 5.915 -11.639 -15.244 3.771 0.804 -0.244 -11.506 0.133 6.048
5 8.445 -9.686 -3.216 -5.585 0.817 -0.225 -8.963 0.723 9.168
number of bands 200
4 5.915 -11.639 -15.244 3.769 0.804 -0.244 -11.507 0.132 6.047
5 8.445 -9.686 -3.216 -5.587 0.817 -0.225 -8.964 0.722 9.167
number of bands 250
4 5.915 -11.639 -15.244 3.769 0.804 -0.244 -11.507 0.131 6.047
5 8.445 -9.686 -3.216 -5.587 0.817 -0.225 -8.964 0.722 9.167
So that nband=100 can be considered converged within 0.01eV.
At this stage, we know that for the self-energy computation, we need ecutwfn=5.0 ecutsigx=6.0, nband=100 .
6 Convergence on the number of planewaves in the wavefunctions to calculate the screening (ε-1) (optional). Now, we come back to the calculation of the screening. Adequate convergence studies will couple the change of parameters for optdriver=3 with a computation of the GW energy changes. One cannot rely on the convergence of the macroscopic dielectric constant to assess the convergence of the GW energies.
As a consequence, we will define a double loop over the datasets:
ndtset 10 udtset 5 2The datasets 12,22,32,42 and 52, drive the computation of the GW energies :
# Calculation of the Self-Energy matrix elements (GW corrections) optdriver?2 4 getscr?2 -1 ecutwfn?2 5.0 ecutsigx 6.0 nband?2 100The datasets 11,21,31,41 and 51, drive the corresponding computation of the screening :
# Calculation of the screening (epsilon^-1 matrix) optdriver?1 3In this latter series, we will have to vary the three different parameters ecutwfn, ecuteps and nband.
First, we check the convergence on the number of planewaves to describe the wavefunctions, in the calculation of the screening. This will be done by defining five datasets, with increasing ecutwfn:
ecutwfn:? 3.0 ecutwfn+? 1.0
In directory ~abinit/tests/tutorial/Input/Work_gw1, copy the file
../tgw1_6.in, and modify the tgw1_x.files file as usual.
Edit the tgw1_6.in file, and take the time to examine it.
Then, issue :
abinit < tgw1_x.files >& tgw1_6.log &This small job lasts about 15 secs on a PC PIV Intel 2.2 GHz.
Edit the output file. The number of plane waves used for the wavefunctions in the computation of the screening is mentioned in the fragments of output:
EPSILON^-1 parameters (SCR file): dimension of the eps^-1 matrix 169 number of plane-waves for wavefunctions 59
Gathering the macroscopic dielectric constant and GW energies for each planewave set, one gets:
dielectric constant = 101.5301
dielectric constant without local fields = 147.3095
number of plane-waves for wavefunctions 59
4 5.915 -11.639 -15.244 3.799 0.806 -0.241 -11.483 0.156 6.071
5 8.445 -9.686 -3.216 -5.555 0.816 -0.225 -8.939 0.747 9.193
dielectric constant = 99.5265
dielectric constant without local fields = 143.7208
number of plane-waves for wavefunctions 113
4 5.915 -11.639 -15.244 3.769 0.804 -0.244 -11.507 0.132 6.047
5 8.445 -9.686 -3.216 -5.582 0.815 -0.226 -8.961 0.725 9.170
dielectric constant = 98.2598
dielectric constant without local fields = 142.5982
number of plane-waves for wavefunctions 137
4 5.915 -11.639 -15.244 3.762 0.801 -0.248 -11.514 0.125 6.040
5 8.445 -9.686 -3.216 -5.588 0.815 -0.227 -8.967 0.720 9.165
dielectric constant = 97.6265
dielectric constant without local fields = 142.1664
number of plane-waves for wavefunctions 169
4 5.915 -11.639 -15.244 3.759 0.804 -0.244 -11.516 0.123 6.038
5 8.445 -9.686 -3.216 -5.590 0.815 -0.227 -8.969 0.717 9.163
dielectric constant = 96.4286
dielectric constant without local fields = 140.5466
number of plane-waves for wavefunctions 259
4 5.915 -11.639 -15.244 3.760 0.803 -0.245 -11.515 0.124 6.039
5 8.445 -9.686 -3.216 -5.592 0.815 -0.227 -8.970 0.717 9.162
So that ecutwfn=4.0 (npwwfn=113) can be considered converged within 0.01eV.
7 Convergence on the number of bands to calculate the screening (important). This convergence study is rather important. It can be done at the same time as the convergence study for the number of bands for the self-energy. Note that the number of bands used to calculate both the screening and the self-energy can be lowered by a large amount by resorting to the extrapolar technique (see the input variable gwcomp).
Second, we check the convergence on the number of bands in the calculation of the screening. This will be done by defining five datasets, with increasing nband:
nband11 25 nband21 50 nband31 100 nband41 150 nband51 200
In directory ~abinit/tests/tutorial/Input/Work_gw1, copy the file ../tgw1_7.in, and modify the tgw1_x.files file as usual. Edit the tgw1_7.in file, and take the time to examine it.
Then, issue :
abinit < tgw1_x.files >& tgw1_7.log &This small job lasts about 22 secs on a PC PIV Intel 2.2 GHz.
Edit the output file. The number of bands used for the wavefunctions in the computation of the screening is mentioned in the fragments of output:
EPSILON^-1 parameters (SCR file): dimension of the eps^-1 matrix 169 number of plane-waves for wavefunctions 113 number of bands 25
Gathering the macroscopic dielectric constant and GW energies for each number of bands, one gets:
dielectric constant = 99.5265
dielectric constant without local fields = 143.7208
number of bands 25
4 5.915 -11.639 -15.244 3.769 0.804 -0.244 -11.507 0.132 6.047
5 8.445 -9.686 -3.216 -5.582 0.815 -0.226 -8.961 0.725 9.170
dielectric constant = 100.6436
dielectric constant without local fields = 143.7240
number of bands 50
4 5.915 -11.639 -15.244 3.587 0.804 -0.244 -11.654 -0.015 5.900
5 8.445 -9.686 -3.216 -5.764 0.815 -0.227 -9.110 0.576 9.021
dielectric constant = 101.1764
dielectric constant without local fields = 143.7244
number of bands 100
4 5.915 -11.639 -15.244 3.516 0.804 -0.244 -11.711 -0.072 5.843
5 8.445 -9.686 -3.216 -5.846 0.811 -0.233 -9.179 0.507 8.952
dielectric constant = 101.2028
dielectric constant without local fields = 143.7244
number of bands 150
4 5.915 -11.639 -15.244 3.510 0.804 -0.244 -11.715 -0.077 5.839
5 8.445 -9.686 -3.216 -5.853 0.810 -0.234 -9.186 0.501 8.946
dielectric constant = 101.2128
dielectric constant without local fields = 143.7244
number of bands 200
4 5.915 -11.639 -15.244 3.509 0.803 -0.246 -11.716 -0.077 5.838
5 8.445 -9.686 -3.216 -5.854 0.812 -0.231 -9.185 0.501 8.946
So that the computation using 100 bands can be considered converged within 0.01eV.
8 Convergence on the dimension of the ε-1 matrix (important).
Third, we check the convergence on the number of plane waves in the calculation of the screening. This will be done by defining six datasets, with increasing ecuteps:
ecuteps:? 3.0 ecuteps+? 1.0
In directory ~abinit/tests/tutorial/Input/Work_gw1, copy the file ../tgw1_8.in, and modify the tgw1_x.files file as usual. Edit the tgw1_8.in file, and take the time to examine it.
Then, issue:
abinit < tgw1_x.files >& tgw1_8.log &This small job lasts about 25 secs on a PC PIV Intel 2.2 GHz.
Edit the output file. The number of bands used for the wavefunctions in the computation of the screening is mentioned in the fragments of output:
EPSILON^-1 parameters (SCR file): dimension of the eps^-1 matrix 59
Gathering the macroscopic dielectric constant and GW energies for each number of bands, one gets:
dielectric constant = 102.1281
dielectric constant without local fields = 143.7244
dimension of the eps^-1 matrix 59
4 5.915 -11.639 -15.244 3.684 0.806 -0.241 -11.576 0.063 5.978
5 8.445 -9.686 -3.216 -5.847 0.811 -0.232 -9.180 0.506 8.951
dielectric constant = 101.2712
dielectric constant without local fields = 143.7244
dimension of the eps^-1 matrix 113
4 5.915 -11.639 -15.244 3.559 0.804 -0.243 -11.677 -0.038 5.877
5 8.445 -9.686 -3.216 -5.850 0.811 -0.233 -9.182 0.504 8.949
dielectric constant = 101.2649
dielectric constant without local fields = 143.7244
dimension of the eps^-1 matrix 137
4 5.915 -11.639 -15.244 3.535 0.804 -0.244 -11.696 -0.057 5.858
5 8.445 -9.686 -3.216 -5.846 0.811 -0.232 -9.179 0.507 8.952
dielectric constant = 101.1764
dielectric constant without local fields = 143.7244
dimension of the eps^-1 matrix 169
4 5.915 -11.639 -15.244 3.516 0.804 -0.244 -11.711 -0.072 5.843
5 8.445 -9.686 -3.216 -5.846 0.811 -0.233 -9.179 0.507 8.952
dielectric constant = 101.1384
dielectric constant without local fields = 143.7244
dimension of the eps^-1 matrix 259
4 5.915 -11.639 -15.244 3.517 0.804 -0.244 -11.710 -0.072 5.844
5 8.445 -9.686 -3.216 -5.845 0.811 -0.232 -9.179 0.507 8.953
So that ecuteps=6.0 (npweps=169) can be considered converged within 0.01eV.
At this stage, we know that for the screening computation, we need ecutwfn=4.0 ecuteps=6.0, nband=100.
Of course, until now, we have skipped the most difficult part of the convergence tests: the covergence in the number of k-points. It is as important to check the convergence on this parameter, than on the other ones. However, this might be very time consuming, since the CPU time scales as the square of the number of k points (roughly), and the number of k-points can increase very rapidly from one possible grid to the next denser one. This is why we will leave this out of the present tutorial, and consider that we already know a sufficient k-point grid, for the last calculation.
9 Calculation of the GW corrections for the band gap in Γ. Now we try to perform a GW calculation for a real problem: the calculation of the GW corrections for the direct band gap of bulk Silicon in Γ.
In directory ~abinit/tests/tutorial/Input/Work_gw1, copy the file ../tgw1_9.in, and modify the tgw1_x.files file as usual. Then, edit the tgw1_9.in file, and, without examining it, comment the line
ngkpt 2 2 2 # Density of k points used for the automatic tests of the tutorialand uncomment the line
#ngkpt 4 4 4 # Density of k points needed for a converged calculationThen,
abinit < tgw1_x.files >& tgw1_9.log &This job lasts about 20 minutes on a PC PIV Intel 2.2 GHz. Because it is so long, it was worth to run it before the examination of the input file.
Now, you can examine it.
We need the usual part of the input file to perform a ground state calculation.
This is done in dataset 1 and at the end we print out the density.
We use a 4x4x4 FCC grid (so, 256 k points in the full Brillouin Zone),
shifted, because it is the most economical.
It gives 10 k-points in the Irreducible part of the Brillouin Zone.
However, this k-point grid does not contains the Γ point, and, at present,
one cannot perform calculations of the self-energy corrections
for other k points than those present in the grid of k-points
in the KSS file.
Then in dataset 2 we perform a non self-consistent calculation to calculate the Kohn-Sham structure in a set of 19 k-points in the Irreducible Brillouin Zone. This set of k-points is also derived from a 4x4x4 FCC grid, but a NON-SHIFTED one. It has the same density of points as the 10 k-point set, but the symmetries are not used in a very efficient way. However, this set contains the Γ point, which allows us to tackle the computation of the band gap at this point.
In dataset 3 we calculate the screening. The screening calculation is very time-consuming. So, we have decided to decrease a bit the parameters found in the previous convergence studies. Indeed, ecutwfn has been decreased from 4.0 to 3.6. This is rather innocuous. Also, nband has been decreased from 100 to 25. This is a drastic change. The CPU time of this part is linear with respect to this paramater (or more exacly, with the number of conduction bands). Thus, the CPU time has been decreased by a factor of 4. Referring to our previous convergence study, we see that the absolute accuracy on the GW energies is now on the order of 0.2 eV only. However, the gap energy (difference between valence and conduction states), that is the relative accuracy, is likely correct within 0.02 eV. It is very important to clarify this point: in bulk systems what matters is only the relative accuracy. There is no zero of the energy defined for a bulk system. Hence in these systems one CAN WELL check the convergence only on the relative accuracy on the energies rather than the absolute, by checking the convergence on the band gap for example. This will reduce a lot the values to be found for the convergence parameters. The same holds for 2-, 1-, and 0-dimensional systems if one is interested only on relative energies and is not interested in calculating quantities like the work function.
Finally in dataset 4 we calculate the self-energy matrix element in Γ, using the previously determined parameters.
You should obtain the following results:
k = 0.000 0.000 0.000
Band E0 VxcLDA SigX SigC(E0) Z dSigC/dE Sig(E) E-E0 E
4 5.915 -11.238 -12.425 0.861 0.771 -0.296 -11.489 -0.251 5.664
5 8.445 -10.049 -5.858 -3.690 0.772 -0.296 -9.662 0.387 8.833
E^0_gap 2.530
E^GW_gap 3.169
DeltaE^GW_gap 0.639
So that the LDA energy gap in Γ is about 2.53eV, while
the GW correction is about 0.64eV, so that the GW band gap found is 3.17eV.
One can compare now what have been obtained to what one can get from the litterature.
EXP 3.40 eV Landolt-Boernstein LDA 2.57 eV L. Hedin, Phys. Rev. 139, A796 (1965) LDA 2.57 eV M.S. Hybertsen and S. Louie, PRL 55, 1418 (1985) LDA (FLAPW) 2.55 eV N. Hamada, M. Hwang and A.J. Freeman, PRB 41, 3620 (1990) LDA (PAW) 2.53 eV B. Arnaud and M. Alouani, PRB 62, 4464 (2000) LDA 2.53 eV present work GW 3.27 eV M.S. Hybertsen and S. Louie, PRL 55, 1418 (1985) GW 3.35 eV M.S. Hybertsen and S. Louie, PRB 34, 5390 (1986) GW 3.30 eV R.W. Godby, M. Schlueter, L.J. Sham, PRB 37, 10159 (1988) GW (FLAPW) 3.30 eV N. Hamada, M. Hwang and A.J. Freeman, PRB 41, 3620 (1990) GW (PAW) 3.15 eV B. Arnaud and M. Alouani, PRB 62, 4464 (2000) GW (FLAPW) 3.12 eV W. Ku and A.G. Eguiluz, PRL 89, 126401 (2002) GW 3.17 eV present work
The values are spread over an interval of 0.2eV. They depend on the details of the calculation. In the case of pseudopotential calculations, they depend of course on the pseudopotential used. However, a GW result is hardly meaningful beyond 0.1 eV, in the present state of the art. But this goes also with the other source of inaccuracy, the choice of the pseudopotential, that can arrive up to even 0.2 eV. This can also be taken into account when choosing the level of accuracy for the convergence parameters in the GW calculation.
Finally, it is possible to calculate a full band plot of a system. There are two possible techniques. The first one is based on the use of Wannier functions, to interpolate a few selected points obtained using the direct GW approach. You need to have the Wannier90 plug-in installed. See the directory tests/wannier90, test case 03, for an example of a file where a GW calculation is followed by the use of Wannier90. Another practical way follows from the fact that the GW corrections are quite linear with the energy, for each group of bands. This is evident when reporting on a plot the GW correction with respect to the 0-order LDA energy for each state. One can then simply correct the Kohn-Sham band structure at any point, by using a GW correction for the k-points where it has not been calculated explicitly, using a fit of the GW correction at a sparse set of points.
In order to circumvent the plasmon-pole model, the GW frequency convolution has to be calculated explicitly along the real axis. This is a tough job, since G and W have poles along the real axis. Therefore it is more convenient to use another path of integration along the imaginary axis plus the residues enclosed in the path.
Consequently, it is better to evaluate the screening for imaginary frequencies (to perform the integration) and also for real frequencies (to evaluate the contributions of the residues that may enter into the path of integration). The number of imaginary frequencies is set by the input variable nfreqim. The regular grid of real frequencies is determined by the input variables nfreqre, which sets the number of real frequencies, and freqremax, which indicates the maximum real frequency used.
The method is particularly suited to output the spectral function (contained in file out.sig). The grid of real frequencies used to calculate the spectral function is set by the number of frequencies (input variable nfreqsp) and by the maximum frequency calculated (input variable freqspmax).
The details in the implementation and the justification for the approximations retained can be found in
F. Bruneval, N. Vast, and L. Reining, Phys. Rev. B 74, 045102 (2006).
The only added input variables are
getqps and
irdqps.
These variables concerns the reading of the _QPS file, that contains the eigenvalues and
the unitary transform matrices of a previous quasiparticle calculation.
QPS stands for "QuasiParticle Structure".
The only modified input variables for self-consistent calculations are
gwcalctyp
and bdgw.
When the variable gwcalctyp is in between 0 and 9,
The code calculates the quasiparticle energies only and does not output any QPS file (as in a standard GW run).
When the variable gwcalctyp is in between 10 and 19,
the code calculates the quasiparticle energies only and outputs them in a QPS file.
When the variable gwcalctyp is in between 20 and 29,
the code calculates the quasiparticle energies and wavefunctions and outputs them in a QPS file.
For a full self-consistency calculation, the quasiparticle wavefunctions are expanded in the basis set of the Kohn-Sham wavefunctions.
The variable bdgw now indicates the size of all matrices to be calculated and diagonalized.
The quasiparticle wavefunctions are consequently linear combinations of the Kohn-Sham wavefunctions in between the min and max values of bdgw.
A correct self-consistent calculation should consist of the following runs:
Note that for Hartree-Fock calculations a dummy screening is required for initialization reasons. Therefore, a correct HF calculations should look like
In the case of a self-consistent calculation, the output is slightly more complex:
For instance, iteration 2
k = 0.500 0.250 0.000
Band E_lda <Vxclda> E(N-1) <Hhartree> SigX SigC[E(N-1)] Z dSigC/dE Sig[E(N)] DeltaE E(N)_pert E(N)_diago
1 -3.422 -10.273 -3.761 6.847 -15.232 4.034 1.000 0.000 -11.198 -0.590 -4.351 -4.351
2 -0.574 -10.245 -0.850 9.666 -13.806 2.998 1.000 0.000 -10.807 -0.291 -1.141 -1.141
3 2.242 -9.606 2.513 11.841 -11.452 1.931 1.000 0.000 -9.521 -0.193 2.320 2.320
4 3.595 -10.267 4.151 13.866 -11.775 1.842 1.000 0.000 -9.933 -0.217 3.934 3.934
5 7.279 -8.804 9.916 16.078 -4.452 -1.592 1.000 0.000 -6.044 0.119 10.034 10.035
6 10.247 -9.143 13.462 19.395 -4.063 -1.775 1.000 0.000 -5.838 0.095 13.557 13.557
7 11.488 -9.704 15.159 21.197 -4.061 -1.863 1.000 0.000 -5.924 0.113 15.273 15.273
8 11.780 -9.180 15.225 20.958 -3.705 -1.893 1.000 0.000 -5.598 0.135 15.360 15.360
E^0_gap 3.684
E^GW_gap 5.764
DeltaE^GW_gap 2.080
The columns are